파이썬으로 간단하게 통계 내용을 공부해보아요. 오늘부터 열심히 달려보겠습니다.

포스팅은 타니아이 히로키님의 '누구나 파이썬 통계 분석' 책의 내용을 실습한 것입니다.
감사합니다.

소스코드와 데이터는 아래의 웹페이지에 공개되어 있습니다.
- 한빛출판네트워크(https://www.hanbit.co.kr/support/supplement_list.html)
- 깃허브(https://github.com/ghmagazine/python_stat_sample)
짧고도 긴 여행을 다녀오느라 블로그를 잠시 쉬었습니다.
이제 다시 시작하는 마음으로 포스팅을 하겠습니다.
지난 포스팅까지 우리는 평균, 분산, 히스토그램, 상자그림 등을 이용하여 1차원 데이터를 정리하는 것을 연습했습니다.
즉, 영어 시험 점수 하나를 이용하였습니다.
이번 포스팅부터는 영어 시험 점수와 수학 시험 점수를 사용한 2차원 데이터 정리를 연습하겠습니다.
1차원 데이터를 정리할 때와 달리, 데이터의 상관성을 파악할 수 있다는 특징이 있습니다.
- 데이터를 불러옵니다.
import pandas as pd
import numpy as np
%precision 3
# pd.set_option('precision', 3)
df = pd.read_csv('/content/drive/MyDrive/python_stat_sample-master/data/ch2_scores_em.csv')
df.head()
- student number를 인덱스로 하기 위해, read_csv 줄에 옵션을 추가해보겠습니다.
df = pd.read_csv('/content/drive/MyDrive/python_stat_sample-master/data/ch2_scores_em.csv',
index_col = 'student number')
df.head()
- 이제 우리가 Ch03에서 사용할 데이터프레임을 만들겠습니다.
- 학생들은 A, B, ...로 이름을 붙이고, 처음 10명에 해당하는 영어 성적과 수학 성적으로 이루어진 데이터프레임입니다.
# 필요한 DataFrame 만들기
en_scores = np.array(df['english'])[:10]
ma_scores = np.array(df['mathematics'])[:10]
scores_df = pd.DataFrame({ 'english' : en_scores,
'mathematics' : ma_scores},
index = pd.Index(['A', 'B', 'C', 'D', 'E',
'F', 'G', 'H', 'I', 'J'],
name = 'student'))
scores_df
3.1 두 데이터 사이의 관계를 나타내는 지표
- 상관관계에 대해서 이야기해보겠습니다.
- 영어 성적이 높으면서 수학 성적이 높은 경향 → 양의 상관관계
- 영어 성적이 높을 수록 수학 성적이 낮은 경향 → 음의 상관관계
- 영어 성적과 수학 성적이 서로 영향을 미치지 않을 때 → 무상관, 상관관계가 없다
- 이와 같은 상관을 수치에 대한 지표로 표현하는 것이 이번 절의 목표입니다.
3.1.1 공분산
- 공분산(covariance)는 분산에 가까운 지표입니다.
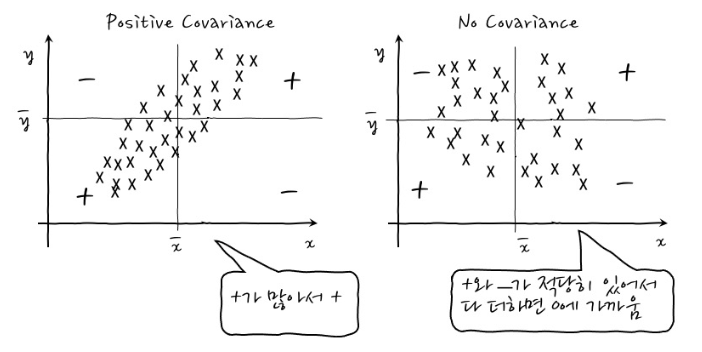
- 공분산은 여럿의 분산이라고 생각하시면 됩니다.
- 그림에서 각각의 점(X표시)에 집중해봅시다.
- 각 점의 x축 평균과의 차이(편차)와 y축 평균과의 차이(편차)의 곱으로 이루어진 면적의 부호를 알아보는 것입니다.
- 그 면적의 부호가 거의 +로 이루어져 있다면 양의 상관관계(공분산이 양의 값), 거의 -로 이루어져 있다면 음의 상관관계(공분산이 음의 값), 그러한 경향성이 보이지 않는다면 상관성이 없다(공분산이 0에 가까움)고 하는 것입니다.
- 이제 함께 공분산을 계산해보겠습니다.
summary_df = scores_df.copy()
summary_df['english_deviation'] = summary_df['english'] - summary_df['english'].mean()
summary_df['mathematics_deviation'] = summary_df['mathematics'] - summary_df['mathematics'].mean()
summary_df['product_deviation'] = summary_df['english_deviation'] * summary_df['mathematics_deviation']
summary_df
- summary_df['product_deviation']의 평균값은 62.8입니다.
- 영어 점수와 수학 점수는 양의 상관관계가 있다고 할 수 있습니다.
- numpy에서는 공분산을 cov 함수로 구할 수 있습니다.
- 다만 반환값은 공분산 행렬 또는 분산공분산행렬입니다.
cov_mat = np.cov(en_scores, ma_scores, ddof = 0)
cov_mat
- 여기서 86은 영어의 분산, 62.8은 영어와 수학의 공분산, 68.44는 수학의 분산을 의미합니다.
3.1.2 상관계수
- 공분산은 결국 편차의 곱, 즉 면적입니다. 따라서 단위가 점수X점수 이렇게 될텐데, 우리에게 익숙하지 않지요.
- 단위에 의존하지 않으면서 상관을 나타내는 지표가 필요합니다. 그것이 바로 상관계수입니다.
- 상관계수는 공분산을 각 데이터의 표준편차로 나눕니다. 단위를 없애기 위함입니다!
- 상관계수는 반드시 -1과 +1 사이의 값을 가집니다.
- 데이터가 양의 상관관계에 놓여 있을수록 +1에 가까워지고, 음의 상관관계에 놓여 있을수록 -1에 가까워집니다.
- 무상관이면 0이 됩니다.
- 또한 상관관계가 -1일 때, +1일 때에는 데이터가 완전히 직선상에 놓입니다.

np.cov(en_scores, ma_scores, ddof = 0)[0,1] / (np.std(en_scores) * np.std(ma_scores))- 위 코드의 반환값은 0.819입니다. 즉, 영어 점수와 수학 점수는 강한 양의 상관관계를 가짐을 알 수 있습니다.
- numpy의 경우, 상관계수는 corrcoef 함수로 계산할 수 있고, 반환값은 상관행렬입니다.
np.corrcoef(en_scores, ma_scores)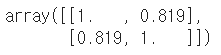
- [0,0] : 영어와 영어의 상관계수(동일 값이니까 상관계수 = 1)
- [1, 1] : 수학과 수학의 상관계수(동일 값이니까 상관계수 = 1)
- [0, 1], [1, 0] : 영어와 수학의 상관계수(강한 양의 상관관계)
- 데이터 프레임도 다음과 같이 간단하게 상관계수를 구할 수 있습니다.
scores_df.corr()
지금까지 너무 수고 많으셨습니다.
다음 시간에는 시각화 연습을 하겠습니다.
감사합니다.
'Python > 통계분석' 카테고리의 다른 글
| [누구나 파이썬 통계분석]_Ch02.1차원 데이터 정리_시각화 (1) | 2024.01.13 |
|---|---|
| [누구나 파이썬 통계분석]_Ch02.1차원 데이터 정리_도수분포표 (0) | 2024.01.11 |
| [누구나 파이썬 통계분석]_Ch02.1차원 데이터 정리_정규화 (1) | 2024.01.08 |
| [누구나 파이썬 통계분석]_Ch02.1차원 데이터 정리_산포도 지표 (1) | 2024.01.08 |
| [누구나 파이썬 통계분석]_Ch02. 1차원 데이터 정리_대푯값 (1) | 2024.01.05 |



